Squaring

Two Digit Numbers

Think of a random integer between 1 and 100.
37?
Hmm.. one of the most impressive feats in mathematics is squaring a number.
First, take a look at the following chart:

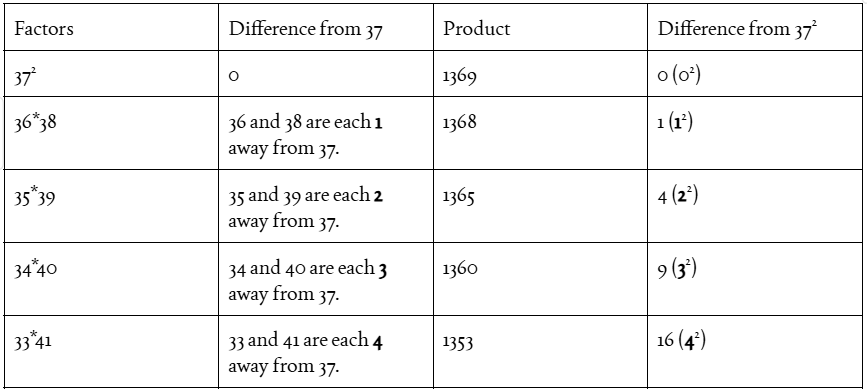
Notice something? If you take two numbers that sum to 37*2 = 74, which each have a difference of x from 37 (either they are larger than or smaller than 37), 372 is x2 away from the product of those two numbers! To calculate 372, we could instead calculate 34*40, a much easier product, then add 9 to calculate 372! As you can test out yourself, this trick works with any integer, regardless of how large or small it is.
So, as seen above, the trick is to round up or down to a multiple of ten, which in our case was 40 but could have been 30 (paired with 44). Both work though!

Special Cases

What if we use this trick to square 35? We would then use the product 30 * 40, which means the two multiples of ten are grouped together, further simplifying your calculations.
What about a number in the 90s? Even though your audience may think that squaring a number like 94 is very difficult, you can take 100 as one of the numbers (and 88 as the other). Multiplying them is extremely simple (just add two zeros behind 88)!

Squaring 3-digit numbers

You guessed it! This trick works for 3-digit numbers too!

Example

Take the number 863.
The obvious and straightforward way is to use 900 or 800 as one of the numbers, as they are multiples of 100. Say we use 900. What is the other number? You can easily calculate it by multiplying 63 by 2, then taking the last two digits. Similar to two digit numbers, the two numbers we choose have to add to 863*2 = 1726. Since we already chose 900 as one of the numbers, we have to have 1726-900 = 826 as the other.

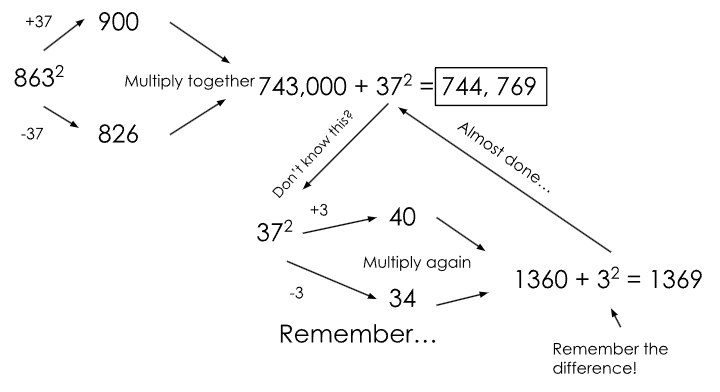
Take a careful look at this chart, a map of the steps we need to follow in order to calculate the answer!